Classe 29-5-2009

Probabilitat condicionada. És aquella en què reduïm l'espai mostral perquè sabem informació extra. La notació que s'ha d'utilitzar és P(A|B)
Treim una carta d'una baralla, si sabem que és una figura, quina és la probabilitat que sigui el rei d'oros? P(rei oros | figura) = 1/12. Sense la informació extra, la pregunta seria: quina és la probabilitat d'obtenir el rei d'oros P(rei oros) = 1/48.

Successos independents són aquells en que el fet que passi un no té cap influència en l'altre.
Per exemple, quan tiram dos daus, el resultat del primer no té cap influència en el resultat del segon (i al revés, també).

Esdeveniments dependents són aquells en que el resultat d'un canvia la probabilitat de que ocorri l'altre.
Treim dues cartes d'una baralla sense reposició, és a dir, no tornam la primera al munt. Llavors, el resultat de la primera té importància per la segona.

Aquí teniu les solucions als exercicis del quadern.
I aquí les solucions dels exercicis per practicar.

Classe 22-5-2009

Fórmula de la unió d'esdeveniments.
P(A U B) = P (A) + P(B) - P(AnB).
A A (vermell i verd) i a B (blau i verd) hi comptam els elements comuns; és a dir, que A conté AnB (verd) i B també conté AnB. Per tant AnB ho hem comptat dues vegades, d'aquí que la restem una.

Successos contraris o complementaris.
És la negació de l'esdeveniment.
El contrari de A="treure un 5" és A'="no treure un 5".
Això, en aquest cas tant obvi, pot semblar inútil, però hi ha ocasions en que simplifica molt els càlculs si s'utilitza la fórmula P(A') = 1 -P(A). És important recordar que junts ens donen l'espai mostral (AUA'=E) i que no tenen elements en comú, són incompatibles (AnA'= buit).
En el dibuix A és la part vermella i "la resta del món" és A', en blau.
Un problema d'exemple:
El 76% del espanyols està preocupat per l'atur i 81% creu que la conjuntura econòmica és dolenta. Sabent que un 72% opina que la conjuntura econòmica és dolenta i està preocupat per l'atur, contestau:
a) Quants ciutadans estan preocupats per les dues qüestions?
b) Quants estan preocupats per l'atur però no per la conjuntura econòmica?
c) A quin percentatge li preocupa només l'atur?
d) Quin és el percentatge de persones que no estan preocupades per cap de les dues coses?
Les dades són semi inventades.

Resposta:
Primer aclarim les dades en notació probabilística. Així, a la llarga, són més fàcil de resoldre els problemes.
A="persones preocupades per l'atur", C="persones preocupades per la conjuntura"
P(A)= 0'76 P(C)=0'81 P(AnC)=0'72 (persones preocupades per les dues coses)
a) Se demana el conjunt de persones preocupades per alguna de les dues coses, és a dir per AuC. Aplicant la fórmula:
P(AuC)= 0'76 + 0'81 - 0'72 = 0'85. Així, un 85% de persones està preocupada per alguna de les dues variables

b) Aquestes són les persones que estan preocupades per l'atur restant les que estan preocupades per les dues coses:
P(AnC')=0'76 - 0'72= 0'04. Per tant un 4% dels enquestats està preocupat només per l'atur

c) És el cas anàleg a l'anterior però canviant A per C
P(A'nC)= 0'81-0'72=0'09. Un 9% de la població està preocupada només per la conjuntura econòmica.

d) Aquí es demana el contrari de AuB, és a dir, no està preocupat per cap de les dues coses
P((AuC)')=1-'085=0'15. Un 15% no està preocupat per cap de les dues qüestions.

Classe 15-5-2009

Probabilitat. Esdeveniments compostos

Taules i diagrames en arbre
Per organitzar la informació quan tiram dos daus podem utilitzar una taula, o bé un diagrama en arbre. En aquest moment, en la introducció de la probabilitat, és clarament més senzill la taula, però heu de tenir en compte que a la llarga és més potent el diagrama en arbre
Unió i intersecció d'esdeveniments
La unió de dos esdeveniments és el conjunt format per tots els elements dels dos conjunts.
La intersecció és el conjunt format per els elements comuns als dos conjunts.

Compatibilitat d'esdeveniments
Successos compatibles (poden passar a la vegada, la intersecció no és buida) i incompatibles (no poden passar a la vegada, la intersecció és buida).
Per exemple si treim una carta a l'atzar d'una baralla i consideram els esdeveniments A="treure figura", B="treure As", C="treure espasa", llavors A i B són incompatibles (no pot sortir una carta que a la vegada sigui figura i as) mentre que A i C són compatibles (figura d'espasa).

Classe 8-5-2009

Introducció a la probabilitat

La probabilitat és una manera de mesura l'incert.
Vam veure els conceptes bàsiques de probabilitat de forma essencialment pràctica:

Experiment determinista vs aleatori
Un experiment és aleatori quan en les mateixes circumstàncies no sempre s'obté el mateix resultat.

Espai mostral
És el conjunt format per tots els resultats possibles. Es denota per U o per E o per omega majúscula.

Esdeveniment simple i esdeveniment compost
Un esdeveniment és simple o elemental quan està format només per un únic resultat possible. Altrament es diu compost.

La llei dels grans nombres
Aquesta llei, experimental, el que diu és que així com anam augmentant el nombre de proves, la freqüència relativa tendeix a estabilitzar-se al voltant d'un nombre. Aquest nombre és la probabilitat de l'esdeveniment. Aquesta probabilitat la podem pensar així com la freqüència relativa si féssim infinits experiments

Regla de Laplace
És una manera molt important de calcular la probabilitat. Només es pot aplicar quan tots els resultats són igualment probables. Aleshores la probabilitat d'un succés és el nombre de casos favorables dividit pel nombre de casos possibles

Classe 3-4-2009

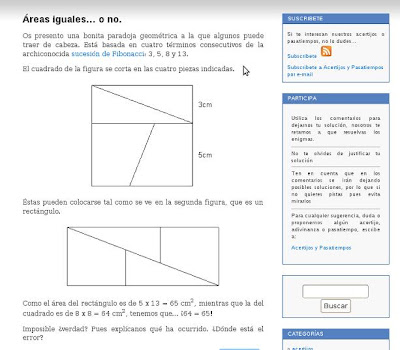
Més àrees (i Pitàgores)

El que vam fer a classe de Leó Tolstoi està tret a partir de librosmaravillosos (concretament d'aquesta pàgina) i una petita variant de la paradoxa del centímetre que desapareix ho podeu trobar aquí (recordau que la que vam fer nosaltres és Marin Gardner)

El pròxim dia 24 de abril, examen. Si teniu dubtes enviau-me un correu.

Classe 27-3-2009

Àrees

En aquesta classe vam començar amb una aproximació a la problemàtica del càlcul d'àrees de qualsevol forma. Una primera manera és quadriculant i comptant (ni que sigui de forma aproximada) quants quadrats ocupa la figura. També podríem utilitzar el mètode d'exhaució que consisteix en anar fent a dins i a fora de la figura polígons de cada vegada més costats dins obtenir una precisió suficient.

La forma per pràctica és aprendre's unes quantes fórmules. A classe vam veure com deduir-les:


Vam practicar un poc per tal de familiaritzar-nos amb la seva utilització. El pròxim dia farem problemes més complicats.

Classe 14-3-2009

L'aparició dels nombres irracionals

El teorema de Pitàgores duu a l'aparició de nombres irracionals o incommensurables, és a dir, que tenen infinit nombre de decimals i no tenen període. Es creu que el seu descobridor va ser n'Hipàs de Metapont (500 a.C.) Per exemple si volem calcular la diagonal d'un quadrat de 4 cm de costats ens donarà l'arrel quadrada de 32, que és un irracional

A pesar que aquest nombres no es poden mesurar directament, sí es poden dibuixar, que és el que vam fer a classe.

I també vam veure alguna aplicació del teorema de Pitàgores. Per deures hi ha el C20.

Classe 6-3-2009

El teorema de Pitàgores

Notes històriques

Es diu teorema de Pitàgores perquè es creu que va ser ell qui el va demostrar per primera vegada. Però el seu origen és desconegut, ja que ha estat present des de els inicis de la història:

A la Xina, a la Índia i a Egipte s'utilitzaven ternes pitagòriques per construir angles rectes. Ho feien utilitzant cordes amb nusos a igual distància.

I els Babilonis també coneixien el teorema. La tableta Plimpton 322 conté sèries numèriques que ho constaten.

Si voleu més informació, podeu consultar un text extens a matematicas.net. I informació sobre la tableta Plimpton 322.

El teorema de Pitàgores.

En un triangle rectangle, cada un dels costats que formen l'angle recte s'anomena catet i el costat que està davant de l'angle recte, hipotenusa.

El que va demostrar Pitàgores és que l'àrea del quadrat construït sobre la hipotenusa és igual a la suma de les àrees dels quadrats construïts sobre els catets.

Casos d'utilització del teorema:

Donats els dos catets, trobar la hipotenusa:

a = 9, b = 12, c = ?
Donat un catet i la hipotenusa, trobar l'altre catet:
a = 5, c = 13, b = ?

Classe 30-1-2009

Mapes i plànols
Heu de tenir ben clar que un mapa o un plànol és un dibuix semblant (en el sentit matemàtic del terme) a la realitat.
Es diu escala a la relació que hi ha entre la realitat i el dibuix. És a dir, a la raó de semblança. Així una escala 1:200 vol dir que el dibuix és 200 vegades més petit que la realitat. També és important la idea de escala gràfica.
Per solucionar els problemes de mapes i plànols hem d'emprar proporcionalitat (per exemple, regles de tres).
I a l'hora de calcular àrees, hem de tenir present que la raó entre les àrees és el quadrat de l'escala.
Per veure el tema de mapes podeu visitar google maps o baixar-vos google earth.



La geometria, universal?
Vam llegir i reflexionar sobre un article de El País.

Els dos pròxims dies farem repàs i exercicis de tot el que hi entra a l'examen de dia 20 de febrer.

Classe 23-1-2009

Relació entre les àrees de figures semblants i la raó de semblança
Heu de tenir molt clar que la raó de les àrees de figures semblants és el quadrat de la raó de semblança. O equivalentment, que la raó de semblança és l'arrel quadrada de la raó de les àrees.
Per veure i aprofundir amb tot això va fer els exercicis 52, 53, 54, 55 i 56

Ampliacions de figures.
Mètode 1. Ampliant les quadrícules (exercici 59)
Mètode 2. Utilitzant una homotècia (que ja hem fet prou exercicis)

El pròxim dia acabarem el tema veient mapes i plànols. Això vol dir que l'examen serà o dia 13 o bé 20 dia de febrer.

Classe 16-1-2009

Semblança de triangles.
Els polígons més senzill són els triangles. És per això que són els més importants. En principi dos triangles són semblants si tenen els angles homòlegs iguals i els costats homòlegs proporcionals. Això vol dir que per comprovar si ho són ens hauríem d'assegurar que tots els costats corresponents són proporcionals i que tots els angles corresponents són iguals.

Criteris de semblança.
No és necessari fer totes les comprovacions anteriors. És suficient en comprovar menys coses.
Per saber si dos triangles són semblants hem d'utilitzar un d'aquests criteris:
- Criteri 1. Un angle igual i els costats que el formen proporcionals.
- Criteri 2. Dos angles iguals.
- Criteri 3. Els tres costats proporcionals.

I si els triangles són rectangles (i per tant ja sabem que tenen un angle igual), els criteris queden:
- Criteri 1. Catets proporcionals
- Criteri 2. Un angle agut igual.
- Criteri 3. Els tres costats proporcionals.

Raó dels perímetres i de les àrees de figures semblants.
Vam dibuixar amb regla i compàs dos triangle semblants de raó de semblança 3, un de costats 12, 9 i 6 i l'altre 4,3 i 2
La raó dels perímetres és 27/9=3; al dibuixar les altures de cada un vam veure que la del primer era 4'5 i la del segon 1'5. Així, l'àrea del primer és A= 12·4'5/2= 27 i la del segon A'= 4·1'5/2 = 3.
La raó de les àrees és per tant 27/3 = 9, que és el quadrat de la raó de semblança. Per què?

Classe 9-1-2009

Hem repassat els exercicis b28 i b29 d'homotècies.
Semblances: hem fet els exercicis b39, b40, b41b i c,b42 i b43

Deures per entregar: apartats c (amb regla i compas) i d de l'exercici B28 (pg 39)
Deures: exercici B30 complet.

I com la setmana anterior, visitau la web del projecte Descartes que explica l'homotècia